Halfedge Class
To help you with developing your own mesh code, here’s a basic implementation of a fairly standard halfedge data structure.
The Halfedge structure is a class parameterized by a vertex type and an
(optional) face type.
template<class Vertex, class Face=int> class Halfedge;
These are the types by which the halfedge will identify it’s origin and
the face it bounds.
As an example, if you have all your vertices
stored in a single array, the Vertex type would presumably be int.
However, you can also choose to use a coordinate vector (e.g., Vec3f)
instead.
Halfedges are generally manipulated using the Halfedge::Handle type.
The standard definition of a Handle is simply as a pointer:
typedef Halfedge *Halfedge::Handle;
Constructors
Individual halfedges can be constructed by specifying their ”origin”:
Halfedge::Halfedge(Vertex org);
This creates a single halfedge, completely isolated from any other
structure. When writing your own code, you will probably not use this
constructor. The create_face() method provides a much more useful
interface for actually building halfedges as part of a mesh.
Accessors
Once created, the origin of a halfedge can be accessed in one of two ways:
Vertex v = e->Org(); // Returns the origin of e
Vertex v = e[0]; // Returns the origin of e
Assuming that it was created as part of a polygon (see below), we can also access its destination,
Vertex v = e->Dest(); // Returns the destination of e
Vertex v = e[1]; // Returns the destination of e
You can of course also make assignments to these values.
e->Org() = v_new;
The Halfedge class itself never examines the values of the vertex and
face data. It simply stores values for use by higher-level code.
Traversal
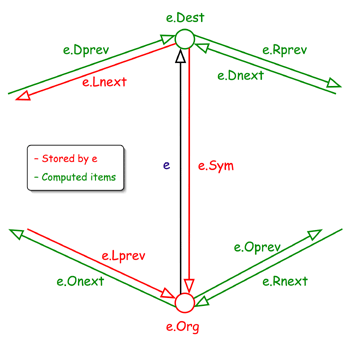
Given a halfedge handle, you can traverse the neighborhood of that edge using a collection of traversal methods. The names of these methods follow those used by Guibas and Stolfi in their paper on the quadedge data structure.
Except along open boundaries, halfedges always come in pairs. Each undirected edge {i,j} is represented by two directed edges (i,j) and (j,i). Given an edge, its symmetric twin going in the opposite direction is accessed as
Handle e2 = e1->Sym(); // Returns NULL if no symmetric edge exists
The Halfedge structure also provides several accessors for other edges
in the immediate neighborhood of a given edge. They all follow the
convention that ”next” means counter-clockwise and ”prev” means
clockwise. Each returns either a valid edge Handle or NULL if no
such edge exists.
e->Lnext(); // Next edge around the face to the left of e
e->Lprev(); // Previous edge around the face to the left of e
e->Rnext(); // Next edge around the face to the right of e
e->Rprev(); // Previous edge around the face to the right of e
e->Onext(); // Next edge around the origin of e
e->Oprev(); // Previous edge around the origin of e
e->Dprev(); // Next edge around the destination of e
e->Dnext(); // Previous edge around the origin of e
Here’s a diagram of the relationship of all these traversal methods to
the edge e.
Working with Halfedges
Since the halfedge constructor creates a halfedge in complete isolation,
it is generally not terribly useful except for internal mesh
manipulation code. In practice, most client code will want to create
halfedges for an entire polygon at a time. This facility is provided by
the Halfedge::create_face method:
template<class Polygon>
static Handle Halfedge::create_face(Polygon& P, Face f=NoFace);
This creates all the halfedges in a counter-clockwise loop around the
given polygon. It returns a handle to one of the edges on this loop.
Along the polygon loop, the Org, Dest, Lnext, and Lprev links
are guaranteed to be valid. All Sym links will by NULL. The
Onext, Oprev, Dnext, and Dprev links will only become valid once
valid Sym links have been established. The optional Face argument
will be used to initialize the Lface data for all the edges.
Given two halfedges (i,j) and (j,i) you can stitch them together so that
they are the Sym of each other using the paste method:
// Creates Sym links between e1 and e2
static void Halfedge::paste(Handle e1, Handle e2);
And cut is the inverse of paste:
// Break the Sym link between e and e->Sym()
static void Halfedge::cut(Handle e);
Note that these are both unconditional operations. It is up to the calling code to verify that the edges being pasted together really ought to be pasted together.